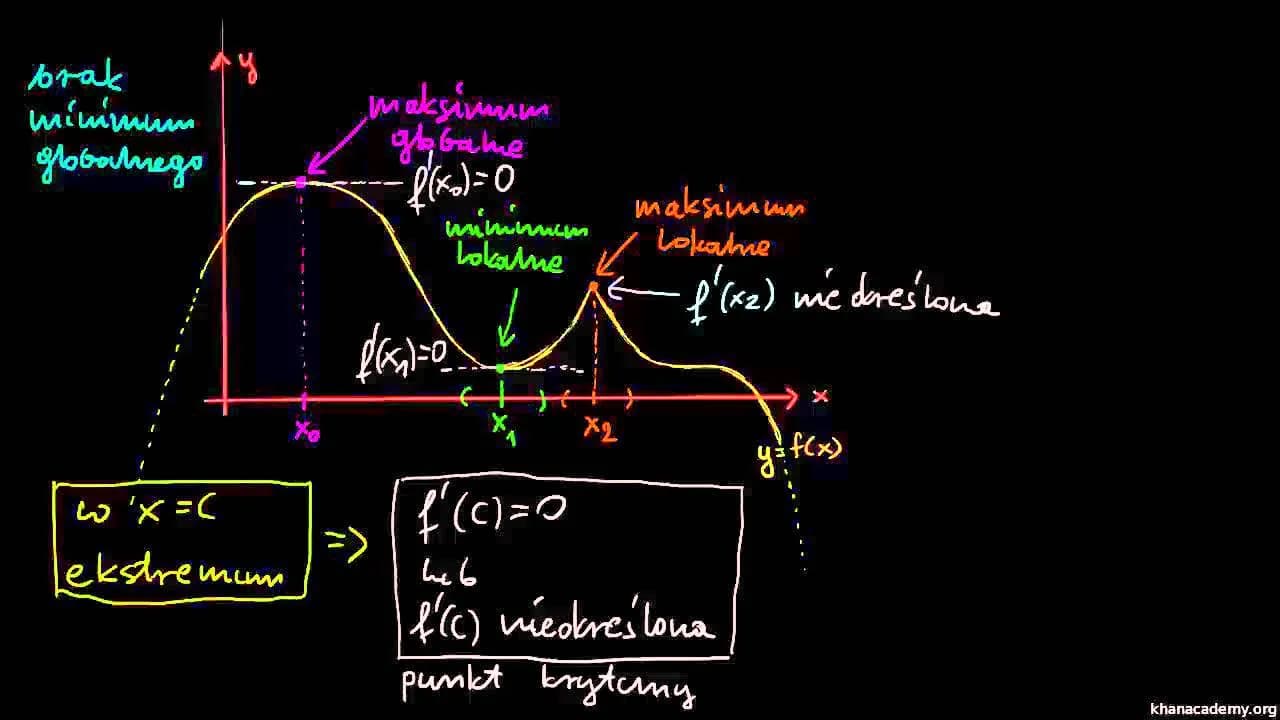
Punkt krytyczny to ważne pojęcie w matematyce i fizyce. W matematyce oznacza punkt, gdzie funkcja ma pochodną równą zero lub nie ma pochodnej. W fizyce to stan, w którym fazy materii się zmieniają, np. ciecz staje się gazem. Punkty krytyczne pomagają nam zrozumieć zachowanie funkcji i substancji w różnych warunkach.
Znajomość punktów krytycznych jest kluczowa w analizie matematycznej i badaniach materiałów. Pozwalają one określić ekstrema funkcji oraz przewidzieć, jak substancje będą się zachowywać pod wpływem zmian temperatury i ciśnienia.
Najważniejsze informacje:
- W matematyce punkt krytyczny to miejsce, gdzie pochodna funkcji jest zero lub nie istnieje
- W fizyce punkt krytyczny oznacza stan przejścia między fazami materii
- Punkty krytyczne są używane do znajdowania ekstremów funkcji
- W termodynamice pomagają zrozumieć zachowanie substancji w różnych warunkach
- Zrozumienie punktów krytycznych jest istotne w analizie matematycznej i badaniach materiałów
Definicja punktu krytycznego w matematyce
Punkt krytyczny w matematyce to kluczowe pojęcie w analizie funkcji. Oznacza miejsce, gdzie funkcja zmienia swoje zachowanie w istotny sposób. To punkt, w którym pochodna funkcji może nie istnieć lub przyjmować wartość zero.
Znajomość punktów krytycznych pozwala matematykom i inżynierom zrozumieć kształt i właściwości funkcji. Są one niezbędne do identyfikacji ekstremów lokalnych, czyli maksimów i minimów funkcji.
- Funkcja jest różniczkowalna i jej pochodna wynosi 0 (punkt stacjonarny)
- Pochodna funkcji nie istnieje w danym punkcie
Znaczenie punktów krytycznych w analizie funkcji
Punkty krytyczne to klucz do zrozumienia zachowania funkcji. Pomagają określić, gdzie funkcja rośnie, maleje lub zmienia kierunek.
W praktyce, analiza punktów krytycznych umożliwia znalezienie ekstremów funkcji. To niezbędne w optymalizacji, gdzie szukamy najlepszych lub najgorszych wyników.
Co ciekawe, nie każdy punkt krytyczny musi być ekstremum. Niektóre mogą być punktami przegięcia, gdzie funkcja zmienia swoją krzywizną, ale nie osiąga maksimum ani minimum.
Wyobraźmy sobie wykres funkcji y = x³ - 3x. Punkt krytyczny występuje przy x = 0 (maksimum lokalne) oraz przy x = ±1 (minima lokalne). Te punkty wyraźnie pokazują, gdzie funkcja zmienia swoje zachowanie.
Punkt krytyczny w fizyce - przejścia fazowe
W fizyce punkt krytyczny oznacza specyficzny stan materii. To moment, gdy substancja balansuje na granicy między dwiema fazami, najczęściej między cieczą a gazem.
W punkcie krytycznym właściwości substancji drastycznie się zmieniają. Znika różnica między cieczą a gazem, tworząc jednolitą fazę o unikalnych cechach. To fascynujące zjawisko ma ogromne znaczenie w badaniach nad materią.
| Właściwość | Przed punktem krytycznym | W punkcie krytycznym |
|---|---|---|
| Gęstość | Różna dla cieczy i gazu | Jednakowa |
| Rozróżnialność faz | Wyraźna granica | Brak granicy |
| Ściśliwość | Niska (ciecz), wysoka (gaz) | Nieskończona |
Temperatura i ciśnienie krytyczne
Temperatura krytyczna i ciśnienie krytyczne to kluczowe parametry definiujące punkt krytyczny. Powyżej tych wartości, gaz nie może być skroplony, niezależnie od przyłożonego ciśnienia.
Znajomość tych parametrów jest niezbędna w przemyśle chemicznym i energetyce. Umożliwia projektowanie wydajnych procesów i bezpieczne przechowywanie substancji w warunkach nadkrytycznych.
Metody identyfikacji punktów krytycznych
Znalezienie punktów krytycznych to kluczowy etap analizy funkcji. Matematycy i inżynierowie używają różnych technik, aby je zlokalizować.
Najpopularniejsza metoda polega na znalezieniu miejsc, gdzie pochodna funkcji równa się zero lub nie istnieje. To proste podejście sprawdza się w wielu przypadkach.
Bardziej zaawansowane techniki wykorzystują analizę numeryczną. Przydają się, gdy funkcja jest zbyt skomplikowana dla metod analitycznych.
- Metoda pochodnej - szukanie miejsc, gdzie f'(x) = 0 lub nie istnieje
- Metoda drugiej pochodnej - badanie zmian znaku f''(x)
- Metody numeryczne - dla funkcji trudnych do zróżniczkowania analitycznie
Narzędzia i programy do analizy punktów krytycznych
Współczesna matematyka korzysta z zaawansowanych narzędzi komputerowych. Programy takie jak Mathematica czy MATLAB znacznie ułatwiają analizę punktów krytycznych.
Te narzędzia nie tylko znajdują punkty krytyczne, ale też wizualizują je na wykresach. To nieoceniona pomoc w zrozumieniu zachowania skomplikowanych funkcji.
GeoGebra to popularny, darmowy program do analizy funkcji. Pozwala na interaktywne badanie punktów krytycznych, oferując intuicyjny interfejs i możliwość tworzenia dynamicznych wykresów.
Zastosowania punktów krytycznych w różnych dziedzinach
Punkty krytyczne mają szerokie zastosowanie w nauce i przemyśle. W ekonomii pomagają przewidzieć optymalne ceny i poziomy produkcji.
Inżynierowie wykorzystują je do projektowania wydajnych maszyn i konstrukcji. Analiza punktów krytycznych pomaga zminimalizować zużycie materiałów przy zachowaniu wytrzymałości.
W fizyce i chemii, zrozumienie punktów krytycznych jest kluczowe dla badań nad zachowaniem materii w ekstremalnych warunkach. To wiedza niezbędna w projektowaniu procesów przemysłowych.
| Dziedzina | Zastosowanie punktów krytycznych |
|---|---|
| Ekonomia | Optymalizacja cen i produkcji |
| Inżynieria | Projektowanie efektywnych konstrukcji |
| Fizyka | Badanie zachowania materii w ekstremalnych warunkach |
| Chemia | Optymalizacja procesów przemysłowych |
Punkty krytyczne w inżynierii i technologii
W inżynierii, punkty krytyczne są kluczowe dla optymalizacji. Pomagają znaleźć najlepsze kształty aerodynamiczne w lotnictwie czy najwydajniejsze profile turbin.
Technologia często opiera się na manipulacji punktami krytycznymi. Na przykład, produkcja półprzewodników wymaga precyzyjnego kontrolowania warunków w pobliżu punktów krytycznych materiałów.
Wpływ punktów krytycznych na właściwości fizyczne substancji
W punkcie krytycznym właściwości fizyczne substancji drastycznie się zmieniają. Granica między cieczą a gazem znika, tworząc unikalną fazę nadkrytyczną.
Ściśliwość substancji w punkcie krytycznym staje się nieskończona. Małe zmiany ciśnienia mogą prowadzić do ogromnych zmian objętości, co ma fascynujące implikacje.
Co ciekawe, w punkcie krytycznym znikają różnice w gęstości między fazami. To prowadzi do niezwykłych zjawisk, takich jak zanik menisku czy opalizacja krytyczna.
Wyobraźmy sobie cylinder z tłokiem, wypełniony cieczą i jej parą. Gdy zbliżamy się do punktu krytycznego, granica między fazami staje się coraz mniej wyraźna, aż całkowicie znika. Substancja staje się jednorodna, wypełniając całą objętość.
Zjawiska nadkrytyczne i ich wykorzystanie
Płyny nadkrytyczne, występujące powyżej punktu krytycznego, mają unikalne właściwości. Łączą zdolność gazów do penetracji z rozpuszczalnością typową dla cieczy.
Te niezwykłe cechy znajdują zastosowanie w przemyśle. Nadkrytyczny CO₂ jest używany do ekstrakcji kofeiny z kawy, a nadkrytyczna woda służy do utylizacji odpadów. To ekologiczne alternatywy dla tradycyjnych rozpuszczalników.
Czy każda funkcja ma punkt krytyczny?
Nie każda funkcja posiada punkt krytyczny. Funkcje liniowe, na przykład y = mx + b, nie mają punktów krytycznych, ponieważ ich pochodna jest stała.
Z drugiej strony, większość funkcji nieliniowych ma przynajmniej jeden punkt krytyczny. Funkcje okresowe, jak sinus czy cosinus, mają nieskończenie wiele punktów krytycznych.
Funkcja wykładnicza y = e^x jest przykładem funkcji bez punktu krytycznego. Jej pochodna (również e^x) nigdy nie równa się zero i zawsze istnieje, więc nie spełnia warunków definicji punktu krytycznego.
Punkty krytyczne a ekstrema funkcji
Punkty krytyczne są kluczowe w znalezieniu ekstremów funkcji. Każde lokalne maksimum lub minimum musi być punktem krytycznym, ale nie odwrotnie.
Test pierwszej pochodnej pomaga określić, czy punkt krytyczny jest maksimum, minimum, czy żadnym z nich. Zmiana znaku pochodnej wokół punktu wskazuje na ekstremum.
Warto pamiętać, że niektóre punkty krytyczne mogą być punktami przegięcia. W takich przypadkach funkcja zmienia kierunek krzywizny, ale nie osiąga ekstremum lokalnego.
Wyobraźmy sobie wykres funkcji y = x³. Punkt krytyczny występuje przy x = 0. To punkt przegięcia, gdzie funkcja zmienia krzywizną z wklęsłej na wypukłą, ale nie jest to ani maksimum, ani minimum.
Kluczowa rola punktów krytycznych w matematyce i fizyce
Punkty krytyczne stanowią fundament analizy matematycznej i fizyki. W matematyce pozwalają zrozumieć zachowanie funkcji, identyfikując miejsca, gdzie zmienia ona swój charakter. To narzędzie niezbędne do znajdowania ekstremów funkcji i optymalizacji w różnych dziedzinach nauki i techniki.
W fizyce punkt krytyczny oznacza wyjątkowy stan materii, gdzie zacierają się różnice między fazami. Zrozumienie zjawisk zachodzących w temperaturze krytycznej i pod ciśnieniem krytycznym otwiera drogę do innowacyjnych zastosowań w przemyśle i technologii.
Badanie punktów krytycznych wymaga zaawansowanych narzędzi i metod, od klasycznej analizy matematycznej po nowoczesne symulacje komputerowe. Ich wszechstronne zastosowania, od ekonomii po inżynierię, podkreślają uniwersalność i znaczenie tego pojęcia w naukach ścisłych i przyrodniczych.